Von links nach rechts: Aus einem Würfel ein Tetraeder schnitzen, dieses um 90° drehen (Stella Octangula) und kopieren und schließlich den Durchschnitt bilden (Oktaeder).
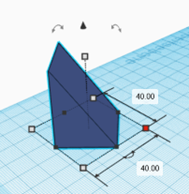
Wir starten mit einem Würfel der Kantenlänge 20. Dazu wählen wir ein dreiseitiges Prisma mit den Maßen 40 x 40 x 40 (Bild 1, unten), drehen dieses um 45° um die lotrechte Achse (Bild 2, unten) und skalieren dieses anschließend in den beiden ebenen Hauptrichtungen wieder auf 40 x 40 (Bild 3, unten). In Folge lässt sich das Prisma exakt an einer Diagonale der Grundfläche des Würfels ausrichten. Durch Spiegelungen und Drehungen dieses Prismas könne drei geeignete Kopien hergestellt werden (Bild 4, unten). Die vier Prismen werden zu Bohrungen gemacht und nach Gruppierung erhalten wir das Tetraeder.
Kopieren und verdrehen des Tetraeders um 90° (und eventuell umfärben eines der Tetraeder) liefert die Stella Octangula. Bilden wir nun den Durchschnitt der beiden Tetraeder mittels doppelter Differenz 𝐴∩𝐵=𝐴\(𝐴\𝐵), so erhalten wir das Oktaeder.
3D-Drucke der Objekte:

TinkerCAD im AR-Modus (Augmented Reality) am iPad:






Comentarios